Bayesian Hierarchical Modeling

In my last post I showed how, when faced with limited data, you can use Empirical Bayes (EB) to better evaluate a players three-point shooting. We can apply this same technique to NCAA three-point shooting across top projects in the upcoming NBA draft.

name	team	3p% (eb)	3p%	3pm	3pa
Anthony Edwards	Georgia	0.312	0.294	72	245
James Wiseman	Memphis	0.329	0.000	0	1

James Wiseman, who missed his only three-point attempt has an EB estimate of 32.9%. His actual shooting percentage had very little impact on his EB estimate. Essentially his percentage was fully regressed to the empirical prior (i.e. league average).

We can see that Wiseman had an EB estimate higher than Anthony Edwards (31.2%), even though Edwards had a higher 3P% (29.4%) - but do we really think Wiseman is a better three-point shooter? What else do we know about these players?

As a Bayesian, we should define our priors about three-point shooting.

1. Good shooters are good shooters¹ (i.e. Higher FT% = Higher 3P%)
2. You only get to shoot 3s if you can - there are always exceptions (i.e. Higher 3PAR = Higher 3P%)

While still small sample sizes, we can take advantage of having slightly more data on FT% and 3PAR - let's see how Wiseman and Edwards stack up in these other areas.

name	team	ft%	3par
Anthony Edwards	Georgia	0.772	0.485
James Wiseman	Memphis	0.704	0.039

Edwards was a better free-throw shooter (77.2% vs. 70.4%). He also had a significantly higher 3PAR (0.485 vs. 0.039). Based on these additional data points, our assumption is that Edwards is probably a better three-point shooter.

Now how can we factor this additional information into our prior…Bayesian hierarchical modeling!

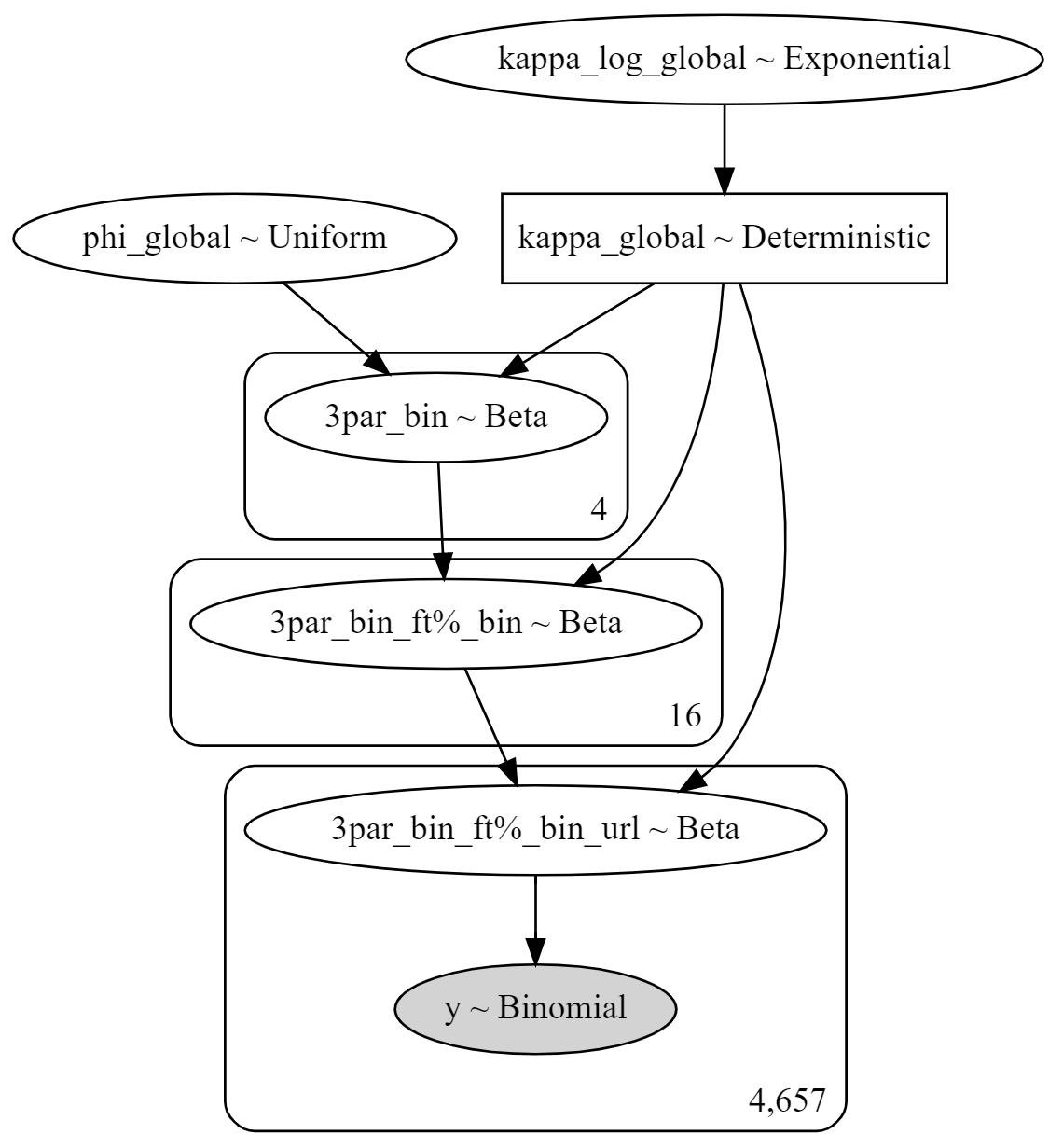
Bayesian hierarchical modeling is a statistical model written in multiple levels (hierarchical form) that estimates the parameters of the posterior distribution using the Bayesian method. The sub-models combine to form the hierarchical model, and Bayes' theorem is used to integrate them with the observed data and account for all the uncertainty that is present.

There are many different ways to approach hierarchical modeling. You could extend our previous empirical bayes approach as described here (which might include using the ebbr package). However, if you are anything like me, once you get a taste of Bayesian statistical modeling you will quickly find yourself deep down a rabbit hole - exploring all the different probabilistic programming frameworks out there, such as PyMC and Stan.

For a basic introduction, you can find sports related examples like analyzing NFL 4th down attempts or predicting rugby outcomes. For a more in-depth understanding, I recommend reading more about multilevel modeling, complex hierarchical modeling, or scaling your model via variational inference.

Now back to apply our problem! As I said, there is no single right way to setup a hierarchical model. It is also worth mentioning that I'm relatively new to Baysian modeling so I won't claim to know what is actually best (feedback please!). With that out of the way, one approach is to use a hierarchical prior based on a players FT% and 3PAR quartile. Using PyMC3 I am able to model three-point shooting as a beta binomial distribution (I'll repeat - feedback from any experts please!).

One benefit of using Bayesian modeling tooling, is that with a few lines of code you get pretty charts like this.

You can also calculate a credible interval to see how the expected distribution changes based on your different groups (in our case FT% and 3PAR quartiles).

In the chart above we can see how players with a high FT% and 3PAR (like Anthony Edwards) have a higher credible interval distribution than a player with above average FT% but low 3PAR (like James Wiseman).

name	team	3p% (hierarchical)	3p% (eb)	3p% (actual)	3pm	3pa
Anthony Edwards	Georgia	0.302	0.312	0.294	72	245
James Wiseman	Memphis	0.256	0.329	0.000	0	1

The hierarchical model pulls Wiseman's estimate toward a more informed prior, which makes his three-point shooting estimate now much lower than that of Edwards (25.6% vs. 30.2%).

Below we can see what the hierarchical model infers about 2020 college performances from the ESPN Top 60 in the upcoming draft.

espn	name	team	3p% (hierarchical)	3p% (eb)	3p% (actual)	3pm	3pa	ft%	3par
11	Aaron Nesmith	Vanderbilt	0.455	0.391	0.522	60	115	0.825	0.561
41	Desmond Bane	Texas Christian	0.419	0.381	0.442	92	208	0.789	0.477
18	Saddiq Bey	Villanova	0.418	0.38	0.451	79	175	0.769	0.477
30	Cassius Winston	Michigan State	0.408	0.371	0.432	73	169	0.852	0.409
52	Immanuel Quickley	Kentucky	0.401	0.366	0.428	62	145	0.923	0.438
37	Payton Pritchard	Oregon	0.398	0.369	0.415	88	212	0.821	0.459
29	Jahmi'us Ramsey	Texas Tech	0.395	0.367	0.432	60	139	0.641	0.415
8	Tyrese Haliburton	Iowa State	0.394	0.36	0.419	52	124	0.822	0.508
42	Tyrell Terry	Stanford	0.388	0.36	0.408	62	152	0.891	0.456
44	Jordan Nwora	Louisville	0.387	0.361	0.402	76	189	0.812	0.44
57	Kaleb Wesson	Ohio State	0.38	0.358	0.425	45	106	0.731	0.346
45	Skylar Mays	LSU	0.375	0.352	0.394	50	127	0.854	0.369
16	Devin Vassell	Florida State	0.37	0.356	0.415	44	106	0.738	0.361
53	Killian Tillie	Gonzaga	0.368	0.349	0.4	36	90	0.726	0.391
38	Malachi Flynn	San Diego State	0.366	0.349	0.373	76	204	0.857	0.489
26	Robert Woodard	Mississippi State	0.363	0.352	0.429	30	70	0.641	0.255
25	Kira Lewis	Alabama	0.355	0.344	0.366	56	153	0.802	0.341
6	Obi Toppin	Dayton	0.354	0.345	0.39	32	82	0.702	0.212
39	Grant Riller	Charleston	0.351	0.341	0.362	47	130	0.827	0.286
22	Josh Green	Arizona	0.349	0.338	0.361	30	83	0.78	0.288
43	Elijah Hughes	Syracuse	0.346	0.336	0.342	78	228	0.813	0.491
46	Isaiah Joe	Arkansas	0.345	0.336	0.342	94	275	0.89	0.764
20	Jalen Smith	Maryland	0.345	0.34	0.368	32	87	0.75	0.279
14	Cole Anthony	North Carolina	0.341	0.337	0.348	49	141	0.75	0.409
34	Tre Jones	Duke	0.341	0.34	0.361	39	108	0.771	0.282
50	Cassius Stanley	Duke	0.34	0.338	0.36	31	86	0.733	0.319
21	Nico Mannion	Arizona	0.335	0.329	0.327	53	162	0.797	0.441
24	Jaden McDaniels	Washington	0.334	0.333	0.339	43	127	0.763	0.378
12	Patrick Williams	Florida State	0.327	0.329	0.32	16	50	0.838	0.242
49	Reggie Perry	Mississippi State	0.318	0.329	0.324	23	71	0.768	0.194
33	Devon Dotson	Kansas	0.317	0.323	0.309	38	123	0.83	0.316
28	Tyler Bey	Colorado	0.309	0.34	0.419	13	31	0.743	0.117
51	Paul Reed	DePaul	0.308	0.326	0.308	16	52	0.738	0.147
36	Daniel Oturu	Minnesota	0.306	0.336	0.365	19	52	0.707	0.123
15	Tyrese Maxey	Kentucky	0.305	0.318	0.292	33	113	0.833	0.322
1	Anthony Edwards	Georgia	0.302	0.312	0.294	72	245	0.772	0.485
54	Ashton Hagans	Kentucky	0.296	0.316	0.258	16	62	0.81	0.234
31	Udoka Azubuike	Kansas	0.295	0.33	0.0	0	0	0.441	0.0
7	Isaac Okoro	Auburn	0.293	0.321	0.286	20	70	0.672	0.287
40	Xavier Tillman	Michigan State	0.282	0.319	0.26	13	50	0.667	0.167
27	Isaiah Stewart II	Washington	0.274	0.324	0.25	5	20	0.774	0.059
35	Zeke Nnaji	Arizona	0.267	0.328	0.294	5	17	0.76	0.054
10	Precious Achiuwa	Memphis	0.264	0.33	0.325	13	40	0.599	0.108
32	Vernon Carey, Jr.	Duke	0.264	0.334	0.381	8	21	0.67	0.061
58	Nick Richards	Kentucky	0.263	0.33	0.0	0	0	0.752	0.0
5	Onyeka Okongwu	USC	0.261	0.329	0.25	1	4	0.72	0.014
3	James Wiseman	Memphis	0.256	0.329	0.0	0	1	0.704	0.038

Below are some notable players that I thought stood out:

1. Vernon Carey - He shot a good percentage for a big (38.1%) but he only had 21 attempts and his lower FT% and 3PAR might make us reconsider how much of his shooting was due to luck.
2. Tyler Bey - Similar to Carey, Bey shot extremely well on the season (41.9%) but he only had 31 attempts and with a low 3PAR, the numbers say he might have been closer to a 30.9% shooter over a larger sample.
3. Ashton Hagans - With such a high FT% (81%), the hierarchical model suggests that Hagans had some bad luck and is a better three-point shooter than his percentage (25.8%) would indicate.

In summary, a hierarchical model is more complex than basic empirical bayes - however the added complexity allows us make to more accurately adjust our prior by incorporating additional information.