When should a team shoot to maximize points?

This is a piece from the Possession Timing 101 multi-part series where we will be diving even further into the topic of possession timing as introduced by the research paper: Optimizing End Of Quarter Shot-Timing In The NBA: "Everyone Knows About The 2 For 1, But What About The 3 For 2?" (pdf). Throughout these posts I hope to: review concepts and results from the research, explore ideas not covered in the paper, and share many more visuals. tothemean is the place to read about strategic possession timing in the NBA.

---

When should a team shoot to maximize points?

In our last post we saw how possession ending time can play a significant role in how many future possessions a team will achieve. One thing we didn't address is that not all possessions are equal. For example, would you say the following two possessions are of equal value?

Although both possessions took roughly 3 seconds to get a three-point shot by LeBron I doubt anyone would say these are actually equal in value.

In the stock market, investors don't look to maximize the numbers of shares of stocks they own. Instead investors look to maximize value. Similarly, in the NBA it is not wise to optimize purely for maximizing possessions. Points are the currency of the NBA, which is why teams should look to maximize points relative to their opponent rather than raw number of possessions. As such, we will now focus on the question of: "When should a team shoot to maximize points?".

First, let me introduce a new metric called Point Advantage Probability (PAP):

PAP represents the probability of a team having a point advantage relative to their opponent through the remainder of a quarter for a particular possession end time (exclusive of current possession value¹)

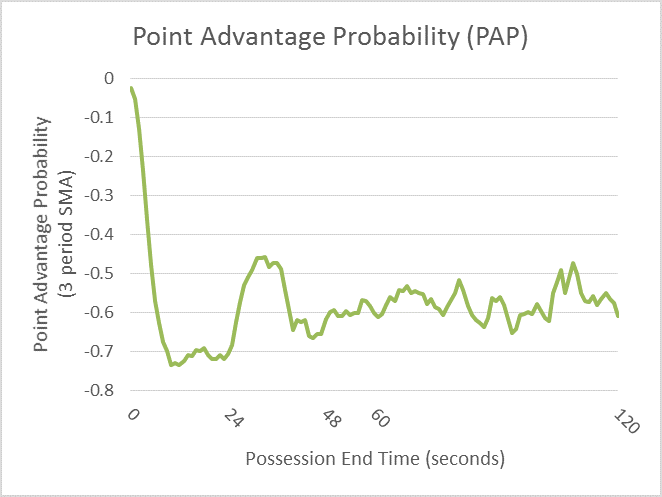
Below you can see how PAP changes over the last 2 minutes of the quarter². The lower the value, the worse probability of outscoring their opponent through the remainder of the quarter for a given possession end time.

In roughly the last 40 seconds there are 3 general themes which I will highlight:

• 0-6 seconds: This time period follows the idea that less time you give your opponent to shoot, the more advantage³ you will have in your favor
• 6-25 seconds: This time period shows a constant disadvantage regardless of how much time is left for the opponent⁴
• 26-40 seconds: "2-for-1" advantage!³ The peak sweet spot in this metric appears to be around 33 seconds

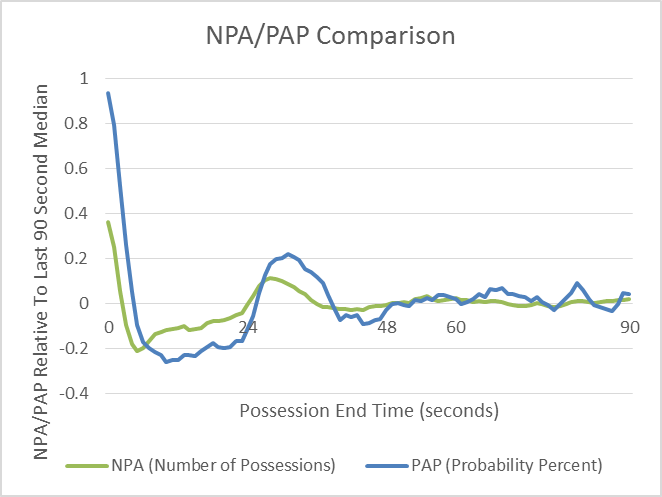
Now lets see how this compares to the question from our last post: "When should a team shoot to maximize possessions?"

The key differences between the two are:

• End of quarter possessions provide less PAP value than NPA value: The NPA values start increasing at ~5 seconds as opposed to PAP which starts at ~10 seconds - When you give the opponent a possession in the final 10 seconds, this will almost always translate to a possession disadvantage but the points disadvantage doesn't appear to be as severe.
• The "2-for-1" range is shifted: The peak NPA value occurs at 28 seconds whereas the peak PAP value occurs at 33 seconds - You may be more likely to get a "2-for-1" at 28 seconds but that doesn't mean the extra possession will be of high value.
• "3-for-2" opportunity?: There seems to be a drop in PAP relative to NPA in the ~42 second range - Could there be opportunities to intentionally try to get out of the low PAP point?⁵

PAP will show the probability of having a point advantage. However if we want to discuss the value of possession timing we need to quantify in terms of points. To do so the paper introduced a metric very similar to PAP called Net Point Differential(NPD)⁶:

NPD represents the average points advantage of a team relative to their opponent through the remainder of a quarter for a particular possession end time (exclusive of current possession value¹)

We can see that NPD shows very similar results to NPA (but with actual point values!):

The key takeaway from this post is: an extra possession doesn't directly translate to points and there are other variables to consider. If you think of a "2-for-1" as ALWAYS DESIRABLE regardless of context then you might be incorrectly modeling your strategy. When maximizing for the wrong variable it doesn't matter how optimal you are, you are setting yourself up for failure. From here on out when we are talk about possession timing strategy, we will be discussing in terms of point value and not number of possessions.

Stay tuned for more posts in the Possession Timing 101 multi-part series.